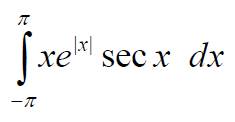Evaluating an integral without actually solving it

Is there any way to obtain the solution for the below integral without solving it?

Student X

Certainly. The function to be integrated is odd in nature.

If we let f(x)= x*e^|x|*sec x, 

then f(-x) = (-x)*e^|-x|*sec (-x) =  -x*e^|x|*sec x = -f(x)

This implies that the graph of f(x) has rotational symmetry about the origin. (A simple example would be the sine curve). Thus, if f(x) is integrated wrt x from -a to a for all a ∈ ℝ, then the result is simply zero.

Hope this helps. Peace.

Best Regards,

Mr Koh